Over the years I have received a lot of emails in response to my post about neural ODEs where people ask for advice on a particular pitfall when applying neural ODEs on regression style problems. So here is a (long overdue) blog post to address that! Code can be found here.
The first lesson of machine learning
If you are a machine learning practitioner I’m sure you’ve been told to “start simple”. Create the simplest possible representative problem and make sure you can solve that before tackling the real deal. This is great advice in basically every setting, but it will always be up to you to figure out what the “simplest possible problem” is. Common strategies include training on a subset of data, using a smaller model, or training on a subset of features. When using neural ODEs the two first options work as you would expect, but if you subset your features you might be in for some tough debugging.
When neural ODEs fail
Let us see an example of failing to fit a neural ODE and then discuss why it fails and possible solutions. Commonly I see people tackling time series problems, and since they are good machine learning practitioners they know they should start simple. So they toss out all features except for one so they can plot the feature against time, and proceed to fit the model (in this example we have a noisy periodic feature). And they are greeted with something like this.
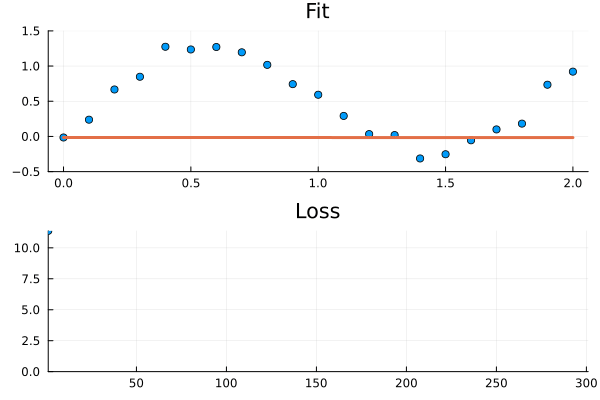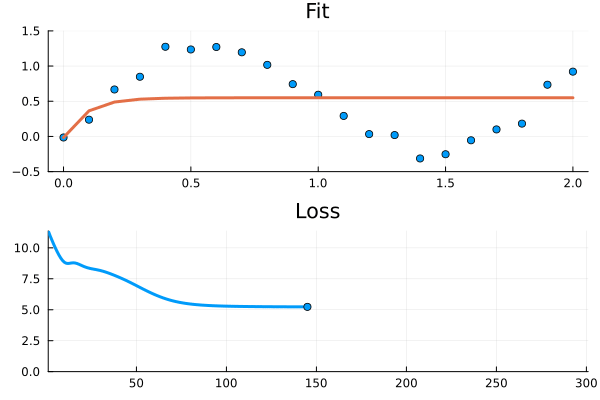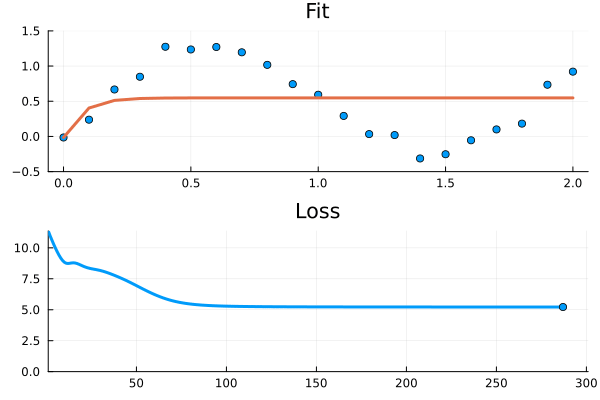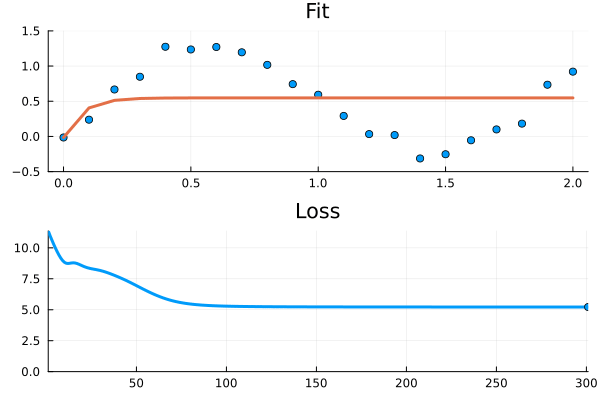
Figure 1: The ODE fails to fit to the relatively simple time series. It looks like it gets stuck in a local minima.
Not what we expected! At first glance it looks like the model got stuck in a really poor local minima. How can this be? Neural ODEs got “neural” in the name, and isn’t “neural anything” supposed to be wildly flexible?
Neural ODEs are not regression models
Neural ODEs do indeed have “neural” in the name and are indeed very flexible in the model class of ODEs. But we get into trouble when thinking of neural ODEs as black-box regression models. They have a lot of structure that constrain the type of data they can model. Recall a neural ODE \(f\) with parameters \(\theta\) has to satisfy
\[ y\prime = f(y; \theta). \]
That is, for each \(y\) there is a deterministic mapping to its derivative \(y\prime\). Hence, to model anything that is not monotonic we would require the derivative to be both negative and positive at the same time. This is of course not possible, so such data cannot be modeled with an ODE. Paradoxically, you might find that the model can fit the data if you add more features back in. How come a more complex problem is easier to solve?
This is because in a higher dimensional feature space it is sometimes possible to find an ODE that fits the data thanks to the additional dimensions they introduce. They give the model space to “loop around itself” so that \(y\) can uniquely identify \(y\prime\). When we remove features we lose these crucial degrees of freedom (There will be visualisations of this later!). But what if there are no more features to add and the ODE still does not fit? Well, then the data is not captured by an ODE and you are better of using another model.
What if I really want ODEs to be black-box regression models?
Okay, just this once. Wish granted. Augmented neural ODE to the rescue! We can add additional dimensions to any neural ODE by introducing auxiliary features for the ODE to “loop around” itself. Since there are no observations for these dimensions they are completely unconstrained and hence very flexible. Doing this gives us something like a black-box regression model, trading interpretability for flexibility.
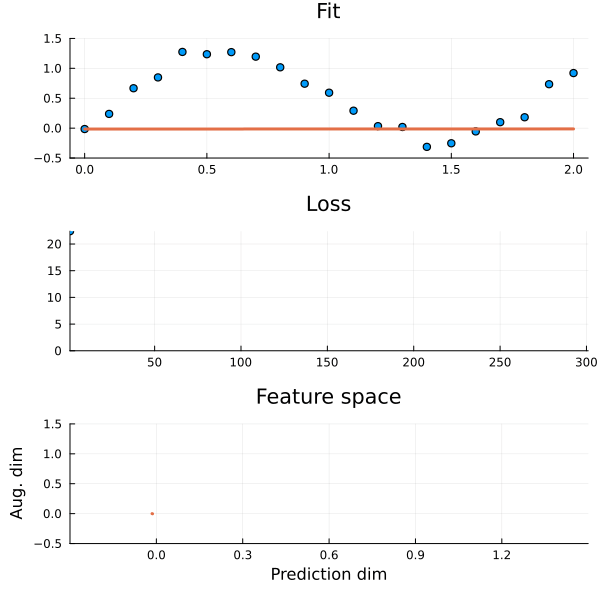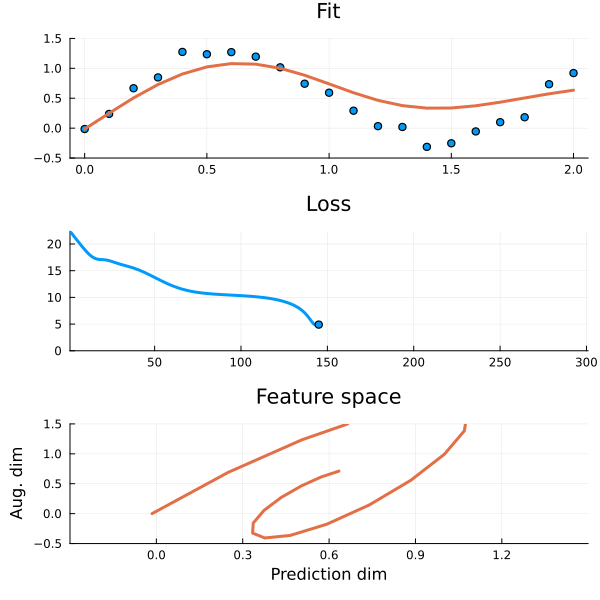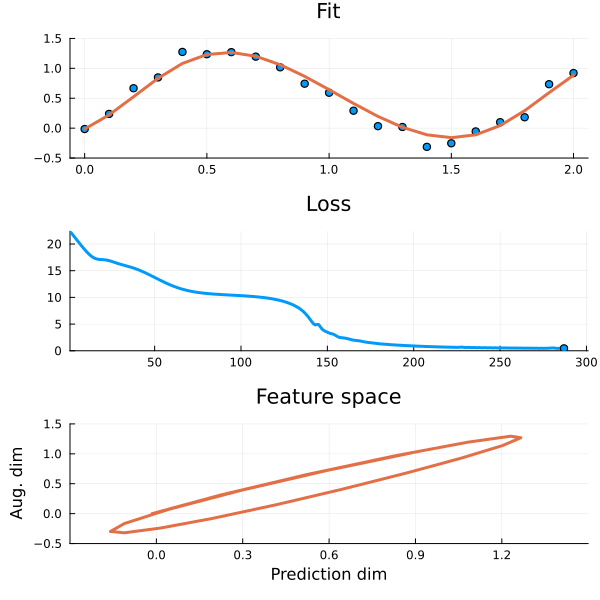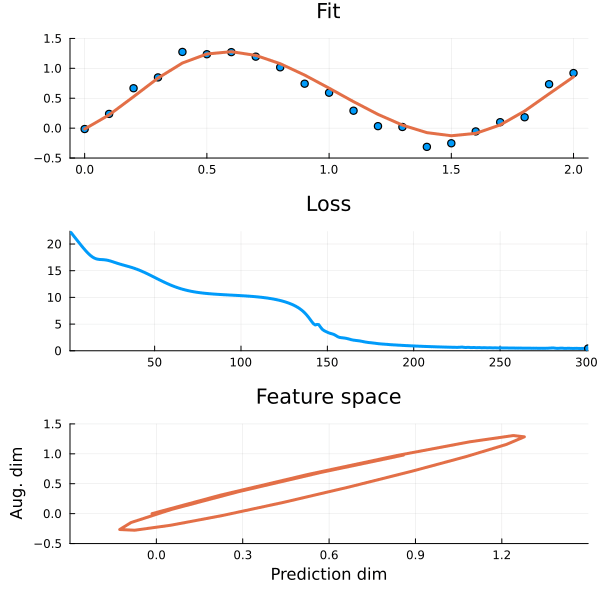
Figure 2: The auxiliary dimension lets the model “loop back around” to capture the periodicity in the data.
Ending Notes
So what have we learned? Firstly, neural ODEs are not regression models. They learn ODEs, with all the structure and constraints they come with. If you think of them as regression models you will inevitably get into trouble since most datasets cannot be modelled with ODEs. However, we can add auxiliary dimensions to any neural ODE to create something like black-box regression models. To put it in a nutshell: If you want to learn an underlying ODE, use vanilla neural ODEs. If you want to fit a flexible regression model, use augmented neural ODEs (or another model altogether).
I hope this post shed some light on what to expect from neural ODEs. Feel free to shoot me an email if you have any questions.